EL CRITERIO DE LOS VOLÚMENES EN EL ESPACIO DE FASES Y SU SUPERIORIDAD AL CRITERIO DE OCKHAM

Introducción
 

Supóngase que se tiene un hecho dado (las manzanas caen) y dos hipótesis pendientes de ser juzgadas que pretenden dar explicación al mismo (la gravedad por un lado o la tendencia natural de las manzanas de cumplir su ciclo vital yendo hacia tierra por otro). Adicionalmente, sucede que es imposible presentar en el juicio experimentos que no se encuentren ya realizados, no existiendo la posibilidad de diseñar un futuro experimento que invalide una de las hipótesis.

Si no existen datos suficientes como para invalidar una de las 2 hipótesis juzgadas, debido a que las dos pueden dar explicación a los fenómenos atendidos, el principio de la Navaja de Ockham establece que es preferible la hipótesis más sencilla sobre la más elaborada a la hora de seleccionar una de las dos hipótesis. Lo cual podría enunciarse como que la hipótesis preferible es la que tiene un menor coste computacional; aquel cuyo algoritmo es más rápido de procesar por una arquitectura computacional dada.

Aunque dos hipotéticas teorías puedan ser equivalentes a la hora de explicar los fenómenos considerados, sino son exactamente equivalentes no ofrecerán las mismas respuestas en toda la gama de cuestiones que se les es posible plantear. Por tanto elegir adecuadamente entre las dos hipótesis aquella que será teoría aceptada, tiene consecuencias en cuanto al conocimiento que se tiene del mundo.

En este texto se planteará un criterio diferente al de la navaja de Ockham para resolver los juicios en los que dos hipótesis de este tipo se pueden ver cautivos. Por otra parte será necesario presentar conceptos como el espacio de fases o la subordinación de teorías para asentar la exposición.

Algo sobre el espacio de fases
 

El espacio de fases es una idea nacida en el desarrollo de la mecánica clásica. Se trata de un volumen  inmerso en un espacio de infinitas dimensiones, en donde uno solo de sus puntos describe completamente el estado físico de todas las partículas del  universo. O dicho de otro modo, en donde cada punto describe un posible fotograma del universo.

Dentro del espacio de fases se pueden formar volúmenes que agrupen puntos que corresponden a fotogramas indistinguibles en cuando dan la misma respuesta a alguna medida realizada por algún aparato o que son equivalentes en cuanto responden de igual modo a una descripción. Estos volúmenes se denominan macroestados, siendo los puntos que contienen los microestados.

El universo evoluciona de un fotograma al siguiente, o de un punto del espacio de fases a otro. Se puede decir que la evolución temporal de un macroestado Z, es una aplicación que transforma el volumen Z en otro volumen Z’. El aumento constante de la entropía impone que ||Z’||>||Z||.
 

La Subordinación de Teorías 

Las teorías sobre el mundo pueden agruparse en escalas, las teorías de más baja escala son aquellas que trabajan a un nivel más fundamental y las que caracterizan un sistema cualquiera con el mayor número de datos. Actualmente en esta escala se encuentra el Modelo Estándar de la física de partículas. En una escala superior a las teorías fundamentales se sitúan las teorías cada vez más generalistas, en donde toman importancia las aproximaciones y cualidades emergentes del comportamiento de la materia a mayor escala. La química y a fisiología animal son respectivamente teorías de mayor escala que la física de partículas

Cualquier nueva hipótesis sobre los sucesos de más alta escala  debe ser congruente con teorías de baja escala que se encuentran aceptadas. Las teorías que están más altas en la escala no pueden modificar las teorías fundamentales, las predicciones de una teoría de alta escala deben de ser consistente con las predichas en baja escala. Ninguna hipótesis de la sociología puede contravenir a las de la biología, ni estas a las de la física.

Criterio de los volúmenes en el espacio de fases (CVEF)
 

Se presentará el criterio que será puesto en comparación con el criterio de Ockham a lo largo del texto. Este criterio debe de aplicarse en la versión maximal o minimal dependiendo de si existe una teoría más fundamental que provee de un espacio de fases de partida o no.

Versión maximal del criterio de volumen en el espacio de fases
 

Siendo el caso más común, se aplica cuando existe una teoría más fundamental aceptada. Puede enunciarse de siguiente modo:

Dadas dos hipótesis será preferible aquella que al aplicarse a la totalidad del espacio de fases del pasado, conduce con mayor probabilidad al hecho presente considerado. 

O equivalentemente:

La hipótesis preferible es la que al aplicarla en retrospectiva sobre el hecho presente, abarca el mayor volumen en el espacio de fases del pasado.
 

Dado que cualquier hipótesis tiene una cualidad reconstructiva de la historia, mediante su uso es posible determinar las condiciones del pasado que han podido originar un hecho en el presente. Desde el macroestado presente que contiene el hecho observado X se aplica la hipótesis para determinar los macroestados pasados que están capacitados para generar dicho hecho X.  El criterio CVEF establece que será preferible la hipótesis que proyecta el hecho presente al mayor volumen pasado.

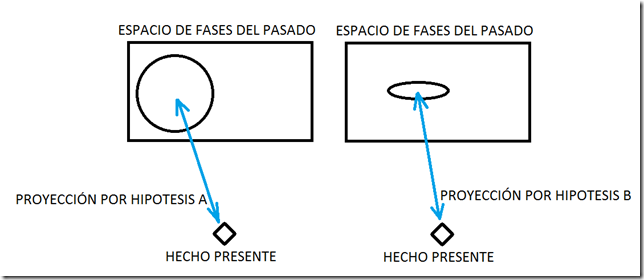
Según CVEF la hipótesis A es preferible porque conduce a un mayor volumen en el espacio de fases pasado.
 

El criterio de Ockham en términos del espacio de fases
 

Traduciendo el criterio de Ockham a términos del espacio de fases, este vendría a decir que la hipótesis preferible es la que proyecta el hecho presente al pasado a un menor coste computacional. Sin ninguna consideración acerca de los volúmenes atribuidos por cada hipótesis.

Según Ockham la hipótesis B es preferible porque determina las condiciones pasadas que dieron lugar al hecho a un menor coste computacional.
 

Diferencia entre CVEF y Ockham
 

Pese a tener enunciados diferentes, y parecer realmente diferentes, pudiera ser que en realidad los criterios CVEF y Ockham fueran equivalentes, que simplicidad y máximo macroestado pasado (en la versión maximal) se presentaran conjuntamente. Se planteará ahora un ejempló en el que no lo son:

Supóngase un universo alternativo que consiste en una habitación cerrada donde existen piezas de construcción esparcidas en su interior. Estas piezas sufren espontáneamente pequeñas sacudidas que las hacen dar saltos y moverse, golpeándose entre ellas a veces. Adicionalmente hay en la habitación un gran bloque formado por piezas de color azul, siendo que las que hay en el suelo son todas de color rojo. Ahora se tienen dos hipótesis a juicio:

1. Al principio las piezas rojas formaban otro bloque pero su agitación térmica los rompió, mientras que las piezas azules están unidas de forma más estable.
2. Al principio las piezas azules no formaban otro bloque, pero la agitación térmica hizo que se construyera dado que liberan energía al hacerlo.

Es trivial que el volumen del espacio de fases del pasado que corresponde con la hipótesis 1 es muchas ordenes de magnitud menor que el que corresponde a la hipótesis 2, dado que hay más configuraciones con piezas desordenadas que ordenadas. Por tanto mediante el empleo del criterio CVEF, debe de prevalecer la hipótesis 2.

A pesar de que a primera vista parece que el criterio Ockham selecciona la hipótesis 1, es difícil establecerlo sin un modo de cuantificar el peso computacional de las propuestas. Para sortear este obstáculo se utilizará un argumento entrópico. A saber; es más difícil programar la formación de un vaso de cristal cualquiera a partir de los fragmentos dispersos, que programar la destrucción de un vaso de cristal en cualquier montón de fragmentos, debido a que se requieren muchas más cifras significativas para la obra de reconstrucción precisa de un vaso. Por contra cualquier empujón reducirá el vaso a fragmentos. Trasladando el argumento al presente experimento de los bloques,  se concluye que el criterio de Ockham selecciona la hipótesis 1. Por tanto ambos criterios no son siempre equivalentes, dado que deciden hipótesis diferentes.

Demostración de la superioridad del CVEF sobre Ockham en la versión maximal
 

Se puede definir superioridad de criterio del siguiente modo:

Un criterio es superior a otro si su probabilidad de acierto es mayor.
 

Se parte de una teoría fundamental aceptada A y de un hecho presente X. La teoría A proyecta el macroestado que contiene el hecho X al macroestado pasado X’. El volumen del macroestado X’ representa también la totalidad del espacio de probabilidades de posibles precedentes de X, siendo que todos los puntos de X’ son equiprobables. Por tanto la probabilidad de que X provenga de un volumen V delimitado en el interior de X’ es P=||V||/||X’||.
 

Se tiene un conjunto de hipótesis de mayor escala (1,2,3…n) que tratan de derivar X desde el pasado, además al proyectar X al pasado producen volúmenes (1’,2’,3’….n’) con probabilidades (||1’||/||X’||,||2’||/||X’||,||3’||/||X’||……||n’||/||X’||). Es trivial que la hipótesis que abarca mayor probabilidad es la de mayor volumen ||n’||. Por tanto el criterio que selecciona hipótesis que tienen mayor probabilidad de ser ciertas es el criterio que selecciona el máximo volumen en el espacio de fases.

Dado que cualquier punto de X’ es origen equiprobable de X, la hipótesis que más volumen abarque en X’ tendrá más probabilidades de ser cierta.

Versión minimal del criterio de volumen en el espacio de fases
 
Se discute ahora si el criterio sigue siendo superior en cuando la teoría aceptada pertenece a una escala mayor, es decir, cuando las hipótesis versan sobre teorías a un nivel más fundamental del de las teorías que se encuentran aceptadas.

En estos casos, son las teorías aceptadas de un nivel más alto las que establecen un espacio de probabilidades X’ a partir del cual se deriva el hecho presente X.  Las hipótesis (1,2,3…n) presentadas sobre el funcionamiento de la escala fundamental deberán de contener a X’ y aportar una nueva totalidad del espacio de fases (1’,2’,3’….n’), en donde a igualdad de capacidad predictiva deberá prevalecerá la ||n’|| menor.

Por tanto la versión minimal de CVEF debe de enunciarse del siguiente modo:

La hipótesis preferible es la que al aplicarla en retrospectiva sobre el hecho presente, genera un espacio de fases con el mínimo volumen total.
 

Demostración de la superioridad del CVEF sobre Ockham en la versión minimal
 

De partida no existe ninguna preferencia por la cual el universo debiera de regirse por una hipótesis determinada, por tanto de origen se acepta la equiprobabilidad Q=1/n de que existan universos con espacios de fases  (1’,2’,3’….n’). La teoría aceptada impone que X’ debe de estar contenido en los (1’,2’,3’….n’) considerados. La probabilidad de que X’ suceda en n’ es ||X’||/||n’||. La probabilidad de que sucedan X’ y n’ a la vez es P=||X’||/(n·||n’||). Por tanto en cuando unos observadores certifican que existe un pasado X’, mayor será la probabilidad que atribuirán a estar contenidos en un universo n en tanto en cuanto menor sea ||n’||.

Dado que los universos regidos por 1’ y por 2’ son equiprobables, una vez se presenta X’ es más probable que se presente en el universo en donde más volumen ocupa.
 

CVEF o Ockham en la primera teoría
 

En los casos anteriores siempre se ha utilizado como pivote una teoría ya existente, sea esta de alto o de bajo nivel. Pero el pivote no existe en cuando se trata de decidir la utilidad de CVEF en seleccionar la primera hipótesis. Podría decirse que el dilema se presenta en elegir entre una teoría simpe o una teoría estable. Pero es posible solucionarlo.

Para salvar este problema se postulará la construcción de un Metaespacio de fases M, el cual contiene todas las permutaciones de toda posible ordenación de información, que incluye por tanto cualquier universo imaginable a modo de macroestados del mismo, siendo cada uno de sus puntos equiprobables. Dado el hecho presente X y un conjunto de hipótesis igual de efectivas que conducen a pasados de diferente volumen (1’,2’,3’….n’), la probabilidad de que provenga de uno de ellos es mayor cuando mayor es ||n’||. Por tanto aplicar CVEF es también criterio superior a Ockham en primera teoría. La demostración en este caso es semejante a la de la versión maximal.

Otros criterios
 

Aunque en el texto se han confrontado CVEF y Ockham, dado que CVEF es equivalente al criterio que selecciona la hipótesis que tiene más probabilidades de ser cierta, es por tanto superior a cualquier otro criterio, en tanto a superioridad se defina en términos de probabilidades de acierto.

FUGA EN EL MODELO DE RICARDO DEL COMERCIO INTERNACIONAL

 

El modelo de Ricardo que data de un relativamente tempranero 1817 es un constructo racional que permite dilucidar en clave favorable el establecimiento del comercio internacional. Un hecho muy importante que respalda este modelo es que es indiferente que exista un país que sea capaz de fabricar cualquier cosa a un coste mucho menor, que incluso los países menos eficientes salen siempre beneficiados del comercio internacional. Esta conclusión, que es correcta en el modelo, descansa sobre la asunción de que cada país obtiene de forma gratuita unos factores de producción que son intransferibles y que pueden producir sin más vino o pan.

Haciendo un añadido

Ineludiblemente, si los factores de producción se valoran en términos de factores intransferibles, él modelo de Ricardo conduciría  a la aceptación del comercio internacional, ahuyentando cualquier fantasma que pudiera aparecer sobre la verdadera bondad que pudiera tener en los países. No obstante cuando los factores de producción son transferibles, la situación puede cambiar completamente.

Ejemplo didáctico

Se tienen dos países que pueden fabricar mesas o sillas. La mano de obra se considera intransferible, habiendo 100 € de mano obra por país, y la estructura de costes es la siguiente:

coste mano de obra	Sillas	Mesas
Marte	2	2
Júpiter	5	3

Sin tener en cuenta más factores, Marte fabricará sillas y Júpiter Mesas, saliendo ambos ganando del comercio internacional. Pero añadamos un nuevo factor que es transferible; la madera. Siendo que hay 100€ de madera por país, la estructura de costes es la siguiente:

coste en madera	Sillas	Mesas
Marte	4	4
Júpiter	7	5

Dado que ahora la madera es comercializable y Júpiter parece derrocharla demasiado en su proceso de fabricación, la solución que aporta la máxima producción puede pasar por que Marte le compre toda su madera a Júpiter y fabrique todos los muebles. Este es un problema resoluble dentro del método Simplex.

• Cuando la madera no se puede comerciar la solución es que marte fabrica 25 sillas y Júpiter 20 mesas
• Cuando la madera se puede comercializar la solución es que marte fabrica 50 mesas o sillas.

Se ve por tanto que la solución de mayor producción pasa por que Júpiter no fabrique nada en absoluto. Es más, cuando se liberaliza el mercado de madera Marte pasa a fabricar 25 sillas extra, por tanto puede entregar 25 sillas por cada 100 de madera que compra sin entrar en perdidas. Mientras que los productores de Júpiter solo pueden pagar 100/7=14,28 sillas por cada 100 de madera que compran, siendo que los propietarios de la madera venderán a Marte.

En definitiva Júpiter se queda sin dar salida a su mano de obra y vendiendo sus factores de producción comercializables hasta agotarse.

PRINCIPIO DE EXCLUSIÓN, TIPOS DE INTERES, INFLACIÓN Y CARRY TRADE

 

Planteamiento

Es ampliamente aceptado que cuando un banco central incrementa el tipo de interés de la moneda, ello posiciona la economía en un escenario más inflacionista que cuando lo reduce. Esto se justifica argumentando que los bancos comerciales estarán dispuestos a pedir prestado más dinero al banco central dado que serán capaces de hacer rentables una mayor cantidad de inversiones de todas las posibles inversiones imaginables. Dado que las inversiones en vías de realizarse compiten por acaparar los mismos recursos escasos, en un principio cabe esperar un incremento de los precios y por tanto inflación. Sin embargo en el texto se encontrarán argumentos en el sentido contrario.

Sobre el rendimiento positivo esperado de las inversiones

No obstante dado que toda inversión económica rentable genera bienes comerciales por un monto superior al valor de la inversión, se aumenta la oferta del mercado en una cuota superior a la base monetaria insuflada, con lo que en segunda instancia provoca deflación. Es de esperar que en una situación estacionaria en donde conviven inversiones jóvenes y las ya maduras, la tasa de inflación sea menor en cuanto menor sea el tipo de interés. A modo de ejemplo ilustrativo, invertir en una fábrica de alfileres genera deflación en los precios después de la inflación primera en el coste de los ladrillos. Claro está que se ha supuesto que el dinero del crédito es destinado íntegramente a inversión, lo cual no es necesariamente cierto.

 

Anécdota: los tipos de interés y la inflación han tenido una correlación positiva en Japón. Aunque los tipos se fijan en función de la inflación, según lo expuesto esta práctica retroalimenta positivamente la tendencia

 

El agotamiento del tipo del interés y el Quantitative Easing QE

La reducción del tipo de interés de una moneda por parte de la autoridad monetaria conduce a un incremento de las deudas en dicha moneda al hacer viables una mayor cantidad de inversiones. Una vez que la flexibilidad de la política monetaria se considera agotada, aún es posible incrementar el monto de los prestamos mediante las herramientas denominadas Quantitative Easing. Llegados a este punto los bancos centrales compran directamente bonos estatales cuyo resultado es asimismo  la reducción de sus costes de financiación y un incremento de las inversiones realizables por los estados. Ambas políticas incrementan el monto total de las inversiones, incorporando masa monetaria nueva al sistema.

La permeabilidad de la moneda a la demanda agregada

No todo dinero afecta igual en la tasa de inflación ligada a los bienes y servicios, o en su participación en la demanda agregada de bienes y servicios DA. Cada agrupación monetaria M tiene una constante K tal que dDA/dt=M·K. Esto es, el dinero que se guarda en los bolsillos tiene una capacidad de participar en la demanda agregada por unidad de tiempo proporcional a una constante K, que es además bastante superior a la K1 de los dineros perdidos en los entresijos del sofá.

Es necesario distinguir estos dineros en una clasificación según su permeabilidad K a la demanda agregada. Una cantidad de dinero puede encontrarse libre (alto K), cómo en el bolsillo de un ciudadano con ganas de gastar o ligada cómo contraparte (muy bajo K). Mientras que el dinero libre puede utilizarse en contrapartida de un bien cualquiera y participar de forma inmediata en la demanda agregada y en la inflación, el dinero que está ligado no puede ya participar en una nueva transacción. Estas son las denominadas garantías, incluidas las propias de la reserva fraccionaria de los depósitos, las propias de los derivados o del mercado de divisas Forex.

Adicionalmente a esta clasificación del dinero en cuanto a su intercambiabilidad, existe la ordinaria propia de los agregados monetarios (M0,M1-M0,M2-M1-M0,…) los cuales también tienen sus propias constantes K de permeabilidad a la demanda agregada DA. En general cuando más bajo M más cerca está del consumo y por tanto participa en mayor medida a la demanda agregada.

Las inversiones en diferentes superficies de permeabilidad a la DA

Los mercados de productos financieros de todo tipo son tan susceptibles a la inversión cómo una fábrica y unas máquinas lo son. No obstante mientras que el gasto de las inversiones fabriles suponen un aumento de la demanda agregada, el gasto en las inversiones financieras parecen tener la cualidad de permanecer cautivas en la topología de la economía financiera, siendo que sus efectos inflacionarios en la economía productiva son menores.

De hecho se utilizará el valor de K de los dineros que participan en una inversión para clasificar estas inversiones en:

• Inversiones en la superficie permeable a la DA, (SP)
• Inversiones en la superficie poco permeable a la DA, (SPP)

La divisa de la nación

La divisa nacional suele estar presente en mayor medida que cualquier otra en la demanda agregada de una nación, así en Europa la demanda agregada está construida mayormente en Euros, aunque también pueda comprarse con otras fórmulas dado el caso. Por tanto la divisa nacional es mayoritaria en la SP. Pero no sucede lo mismo con la SPP de la nación, en donde por ejemplo la divisa Euro puede tener y tiene menor hegemonía, compartiendo su espacio con una cesta de divisas que incluye Dólar, Libra, Yen, etc.

La divisa preferida para la inversión

Existen preferencias en cuando a endeudarse en una moneda con bajos tipos de interés a la hora de realizar una inversión. Se llama carry trade cuando una divisa se sustrae de su ámbito nacional para financiar inversiones en otro lugar, para ello se cambia la moneda en el que se tiene el préstamo por moneda local que tendrá un mayor tipo de interés y se vuelve a comprar la moneda de bajos tipos para terminar de pagar el préstamo . Estos movimientos se realizan entre divisas de diferentes continentes en microsegundos.

El efecto desplazamiento de las divisas por cambio en tipos, principio de exclusión

Cuando una moneda reduce sus tipos de interés, pasa a ocupar las superficies poco permeables de las inversiones de todo el mundo, desplazando a la divisa con mayor tipo que se encontraba en ese lugar y empujándola a la superficie permeable de su nación. Esto sucede porque la superficie impermeable a la DA es por contra la más permeable al tráfico internacional de divisas.

 

Efecto desplazamiento; una bajada de tipos en A conduce a la sustitución de otra moneda B en la superficie de las inversiones impermeable a la DA.

Por tanto una bajada en los tipos de interés provoca un aumento de la masa monetaria permeable fuera de la nación del banco central (BC). El consiguiente incremento en la DA genera inflación al aumentar el consumo y no produce mayor tasa de inversión hasta que no logre revisar los tipos a la baja.

Por contra, cuando un banco central aumenta el tipo del dinero, ello hace que su divisa sea desplazada por otra en la superficie impermeable, conduciéndola hacia la permeable, aumenta la masa permeable, la DA y provocando inflación. Esta es la segunda objeción importante que se presenta al hecho aceptado de que una subida de tipos es contraria a la inflación. Siguiendo el mismo esquema, al bajar los tipos de interés la divisa invade espacios impermeables internacionales, en donde se convierte en demandada, provocando deflación en la nación.

En resumen;  se deben apreciar los efectos comunicantes entre divisas que realiza la superficie impermeable, que junto con la existencia de un principio de exclusión similar al de Pauli configura una mecánica propia del estudio de los acontecimientos.