INTERPRETACIÓN DE LA DERIVADA COMPLEJA

La derivada de una función en variable real es otra función que da para cada punto el valor de la pendiente. La pendiente es sencilla de visualizar cuando se trata de funciones que tienen 1 o 2 variables independientes (V.I). Cuando es una función de 3 V.I, como por ejemplo la presión en el interior de un globo que acaba de explotar, la derivada puede entenderse como cuanto de juntas o separadas están las diferentes curvas isobáricas (de misma presión).

Una función compleja f(z)=f(x+iy)=X+iY necesita 4 dimensiones para representarse. Podría imaginarse como un eje cartesiano de 3 dimensiones, donde en la base se representan los puntos x e y, siendo X la altura e Y la variable representada en forma de isobaras. Adicionalmente, otra forma de representación, siendo que un número complejo puede identificarse por el modulo (distancia al origen) y argumento (ángulo que forma con el eje X). Haciendo la altura el modulo, el argumento se representaría como curvas isobaras.

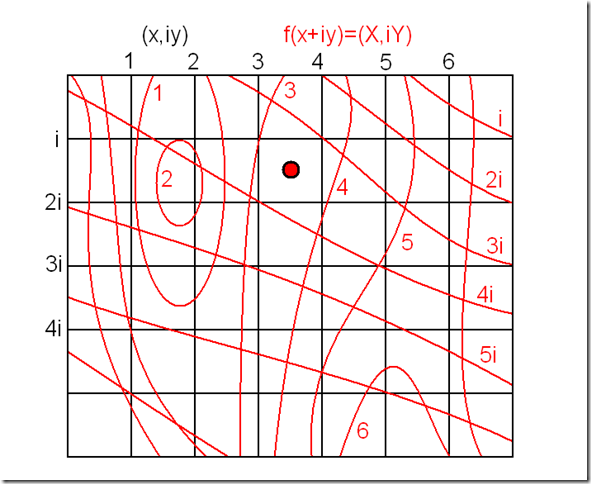
No obstante es posible representar una función compleja f(z) en solo 2 dimensiones. Basta para ello representar sobre el plano (x,iy) una rejilla cuadriculada, cada alambre es una línea que mantiene constante el valor de una de las variables. Ahora se trata de representar una rejilla adicional cuyos alambres son las curvas en donde una de las variables de la imagen (X,iY) se mantiene constante. Si se señala un punto sobre este plano se está señalando a la vez (x,iy) y la imagen f(x,iy). A modo de ejemplo:

Esta forma de representar las funciones complejas servirá para interpretar geométricamente la derivada compleja. 

INTERPRETACION

La definición de derivada expresa:

 

Representando las dimensiones involucradas:

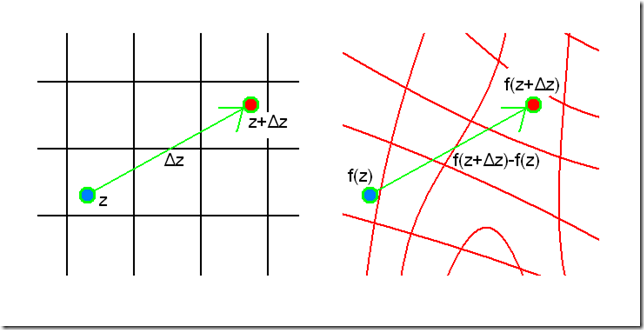
En la figura anterior se ha optado por mostrar por separado la rejilla del espacio origen ortogonal y la rejilla del espacio imagen que antes se mostraban superpuestas. En la derivada se dividen ambos vectores. Para entender la derivada; en primer lugar el espacio imagen (en rojo) se “desarruga”; estirando y curvando su superficie como si fuera de goma, haciendo que las líneas rojas se conviertan en cuadriculas iguales a las del espacio origen, conservando la posición del origen del vector imagen en todo caso. El vector f(z+Δz)-f(z) ha cambiado de tamaño y orientación durante el proceso.

Así f´(z) es el vector por el que hay que multiplicar el vector infinitesimal Δz para que dé el vector imagen. En forma polar f´(z)= R(cos@+isen@), donde R es el factor en el que está incrementado un Δz desde el espacio origen al destino y @ es el ángulo en que las rejillas se curvan en el espacio imagen con respecto al origen.

Es decir, el modulo de la derivada señala el efecto ZOOM que experimenta la rejilla imagen (en rojo) en la dirección en la que se evalúa la derivada. Mientras que el modulo muestra el giro que ha experimentado un alambre puesto en la dirección de la derivada al aplicar la función. 

Por tanto una derivada sin parte imaginaria @=0 proviene de una función escalar, mientras que una derivada con modulo unitario no permitiría que los lados de una rejilla cambiaran su magnitud, aunque si que girasen como si estuvieran articulados. En consecuencia dado que la derivada se entiende en términos de modulo y argumento, es preferible numerar la rejilla que le corresponde en dichas variables.