PARADOJA BANACH-TARSKI EN DOS DIMENSIONES

INTRODUCCIÓN

La paradoja en cuestión dice lo siguiente:

Dada una bola en el espacio tridimensional, existe una descomposición de la bola en un número finito¹ de piezas no solapadas (es decir, subconjuntos disjuntos), que pueden juntarse de nuevo de manera diferente para dar dos copias idénticas de la bola original. Todavía más, el proceso de reensamblaje requiere únicamente remover las piezas y rotarlas, sin cambiar su forma. Sin embargo, las mismas piezas no son "sólidas" en el sentido habitual, sino dispersiones de infinitos puntos.

En resumidas cuentas, dentro de la axiomática ZF de teoría de conjuntos + axioma de elección, es posible hacer pedazos una esfera, y despumes simplemente rotando sus cachos componer dos esferas iguales a la original.

En este texto obtendremos un resultado similar para el caso de un cuadrado. Dividiremos un cuadrado en unas cuantas porciones y cuando las tengamos, con unas rotaciones compondremos dos cuadrados iguales al original.


MULTIPLICANDO LOS CUADRADOS

Primero – clasificar el perímetro

Partiremos de un cuadrado cómo este, cuyo área queremos duplicar.



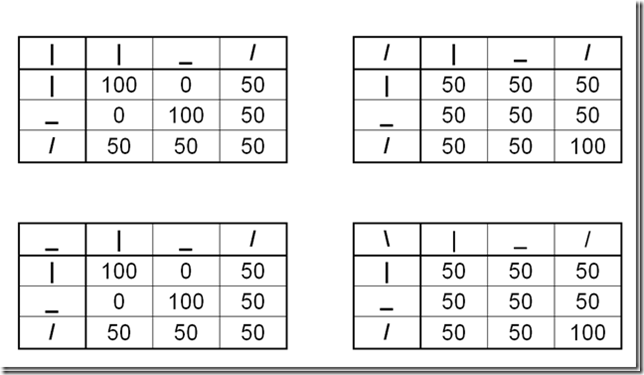
La primera gran tarea a realizar es la de clasificar todos los puntos que hacen el perímetro del cuadrado en tres conjuntos. La forma de clasificar cada punto del perímetro es el siguiente.

Segundo – mediante proyecciones

Para clasificar se siguen los pasos del siguiente algoritmo, se hace pasar un semirrecta que comenzando en el centro del cuadrado y con dirección norte corte al cuadrado en un punto. El primer punto seria el punto Q tal y cómo se obtiene en la imagen. ¿Hemos rotado el cuadrado cómo ultimo paso para obtenerlo? No, por este motivo lo clasificaremos en el conjunto de los Quietos. Veremos más adelante que clasificaremos los puntos del perímetro en tres conjuntos, quietos [Q], Derechas [D] e Izquierdas [I].

Tercero – se pone en marcha el algoritmo

Iteración n=1

Tenemos cuatro opciones para elegir a continuación;

1. Podemos girar el cuadrado a la derecha un numero irracional e+1 (2,718..+1=3,718…) de grados. Recordamos que una vuelta completa tiene 360º. El cuadrado se deja girado, pero no se marca ningún punto de corte con la semirrecta.
2. Podemos girar el cuadrado a la derecha un numero irracional e .A continuación marcamos el lugar de corte de la semirrecta con el cuadrado recién girado. El punto marcado pertenecerá al conjunto [D]. Una ver marcado el punto el cuadrado vuelve a la posición original y n=1.
3. Podemos girar el cuadrado a la izquierda un numero irracional e+1 (2,718..+1=3,718…) de grados. Recordamos que una vuelta completa tiene 360º. El cuadrado se deja girado, pero no se marca ningún punto de corte con la semirrecta.
4. Podemos girar el cuadrado a la izquierda un numero irracional e .A continuación marcamos el lugar de corte de la semirrecta con el cuadrado recién girado. El punto marcado pertenecerá al conjunto [I]. Una ver marcado el cuadrado vuelve a la posición original y n=1. 

Cuarto – infinitas iteracciones

Vimos que en la primera iteración sumábamos los grados de giro eran e+1 para las opciones 1 y 3. En la siguiente iteración en estas opciones el giro sera de e+0,1. En general para la n-sima iteración el giro para las opciones 1 y 3 será de e+(10/10^n). Este engorro es simplemente para conseguir que la clasificación de cada punto en un conjunto sea unica.

Con esto en mente, la iteración n=2, realizada sobre como ha quedado rotado el cuadrado tras n=1, volverá a plantear las mismas 4 opciones. Con las mismas consecuencias. Vemos que solo sobreviven a la siguiente iteración si elegimos la opción 1 y 3. Las otras conducen a marcar un punto y volver al comienzo.

Quinto – encontrando los puntos perdidos

Después de haber realiza infinitas iteraciones, es hora de ir encontrando los puntos que no han quedado marcados, que son infinitos innumerables. Para ello vamos girando el cuadrado hasta que la semirrecta del norte marque el punto que estaba perdido. Apuntando el punto en el conjunto [Q] de los quietos.

Una vez marcado este punto se vuelve a poner en marcha las iteraciones n=1. Esta posición del cuadrado sera la nueva a la que se volverá después de haber marcado el punto.

Ejecutado el algoritmo otra infinidad de veces, volvemos a girar el cuadrado hasta encontrar un nuevo punto perdido y marcándolo en el conjunto [Q]. Proseguimos de este modo hasta que todos los puntos del cuadrado estén clasificados en [Q], [D] o [I].

¿Cómo es posible ejecutar un algoritmo infinito, que contiene una subrutina que es ademas infinita? No es posible, pero el axioma de elección nos permite adelantar que estos puntos serán marcados sin ejecutar el algorimo, y es lo que nos interesa.

Sexto – una matricula para cada punto

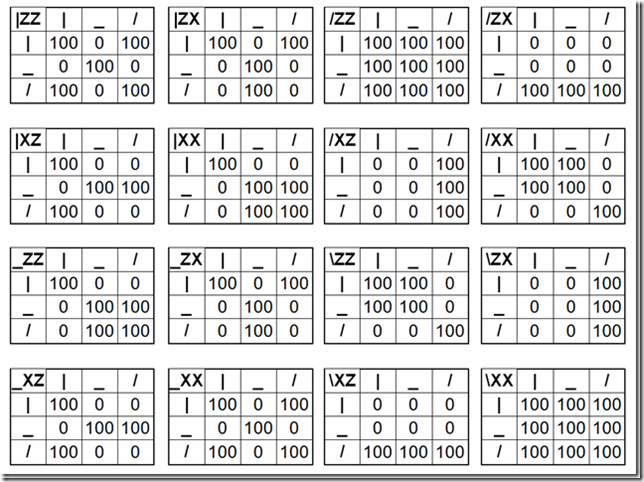
Una forma de identificar cada punto es mediante la secuencia de movimientos izquierda o derecha que se han realizado para alcanzarlo. Por ejemplo el primer punto del ejemplo seria el punto {Q}, si en la siguiente iteración hubiéramos movido el cuadrado a la derecha el punto resultante seria {D,Q}, si en la tercera elegimos mover a la izquierda sería {I,D,Q}. Vemos que los movimientos se escriben de derecha a izquierda. Esto será muy importante más adelante.

Séptimo – extrayendo los conjuntos

Extraeremos del cuadrado los tres conjuntos de puntos. En principio el perímetro tendría que ser la suma de los tres. De modo que, por ejemplo, el área delimitada por el polígono de infinidad de vértices en el cuadrado [Q] no podrá ser igual al área del cuadrado original.



Octavo – las matriculas de cada conjunto

¿Cual es la forma de las matriculas de todos los puntos del cuadrado original? Sabemos que lo constituyen aquellos terminados quietos, a izquierdas y a derechas. Tendran esta forma entonces;

{Q,Q,Q…},{Q,Q,D…},{Q,Q,I…},…….
{D,Q,Q…},{D,Q,D…},{D,Q,I…},…….
{I,Q,Q…},{I,Q,D…},{I,Q,I…},………

¿cual es la matricula de los puntos que pertenecen a I? Sabiendo que terminan en un giro a izquierdas, tienen que tener esta forma;

{I,Q,Q…},{I,Q,D…},{I,Q,I…},………
{I,D,Q…},{I,D,D…},{I,D,I…},………
{I,I,Q…},{I,I,D…},{I,I,I…},………

Noveno – rotando un conjunto se obtiene el total

Ahora vamos a rotar el conjunto [I] hacia la derecha un numero e de grados, esto equivale a añadir una D al final de todas las matriculas. Por tanto el conjunto [I] nos quedaría de la siguiente forma:

{D,I,Q,Q…},{D,I,Q,D…},{D,I,Q,I…},………
{D,I,D,Q…},{D,I,D,D…},{D,I,D,I…},………
{D,I,I,Q…},{D,I,I,D…},{D,I,I,I…},………

Recordamos que tanto la ultima y la penúltima rotaciones en este caso son en ambos casos e y de sentidos contrarios, por tanto se anulan.  El conjunto [I] rotado un angulo e nos queda de la siguiente forma:

{D,I,Q,I…},{D,I,Q,D…},{D,I,Q,Q…},… ={Q,Q,Q…},{Q,Q,D…},{Q,Q,I…},…….
{D,I,D,I…},{D,I,D,D…},{D,I,D,Q…},…={D,Q,Q…},{D,Q,D…},{D,Q,I…},…….
{D,I,I,I…},{D,I,I,D…},{D,I,I,Q…},…={I,Q,Q…},{I,Q,D…},{I,Q,I…},………

Esto es tiene la misma forma de todas las matriculas del cuadrado original. Esto es con este giro hemos obtenido un cuadrado original completo. Y tenemos una copia.

Decimo – la segunda copia

Si hacemos lo mismo con el cuadrado [D], pero girándolo a la izquierda e grados, obtenemos nuevamente las matriculas del cuadrado original completo. Y esta es la segunda copia.

¿que pasa con el cuadrado [Q]?, nos sobra.

Consideraciones finales

1º A pesar de haber empleado en este texto que el infinito es actual, lo cierto es que entiendo que el infinito ha de tomarse como potencial, y desde este punto de vista no puede construirse ninguna paradoja B-T tal cómo se ha hecho.
2º El presente texto de paradoja B-T en dos dimensiones tiene importantes objeciones.

UN EJEMPLO DE VARIABLES OCULTAS EN UN ENTORNO REALISTA Y LOCAL, QUE OFRECE UN RESULTADO POR DEBAJO DE LA DESIGUALDAD DE BELL

1. LA REVOLUCIÓN CUANTICA

La teoría de la mecánica cuántica ha supuesto una herramienta con la que abordar el estudio de la naturaleza allí donde las teorías clásicas fracasaban. Si hubiéramos optado por comprar esta herramienta en un mercado intergaláctico de teorías, el precio que la humanidad hubiera estado dispuestos a pagar sería el de un alto porcentaje de la riqueza mundial, año tras año.

Las teorías físicas clásicas son deterministas; al iniciarse una partida de billar para romper la formación en triangulo de las bolas, la posición en la que quedaran estas tras el golpe está determinada por la velocidad y la dirección con la que se lanza la bola blanca. Si el jugador decide repetir la jugada haciendo exactamente lo mismo, el resultado final será el mismo. En cambio el análisis de dicha partida bajo los dictados de la mecánica cuántica nos dice que lanzamientos idénticos pueden tener resultados muy diferentes.

Este azar es un aspecto realmente incomodo de la teoría, que desde una perspectiva antropocéntrica, nos obliga a afirmar que al universo hay que ponerle una camisa de fuerza antes de que haga algo realmente estúpido e imponerle unas nuevas leyes, que nos gusten más. Lo que parece muy difícil de conseguir, por tanto hay quien opta por conformarse con la perspectiva de que la teoría cuántica es una teoría incompleta, que sus predicciones son probabilistas porque no se tiene en cuenta una realidad ahora oculta que está allí esperando a ser descubiertas. Esta realidad oculta aportaría nuevas variables ocultas, y con ellas sería posible construir una teoría determinista del mundo, que explicaría también los fenómenos que hoy día solo se explican mediante la teoría probabilística. Esta fue la posición de Einstein, que afirmo que Dios no jugaba a los dados.

2. LA DESIGUALDAD DE BELL

En principio, nada parece impedir que pueda construirse una teoría de variables ocultas que permitiera superar nuestro conocimiento actual de la materia, y la gente podía agarrarse a esto para llevar unas vidas normales. O nada parecía impedirlo hasta que un día llego John S.Bell y se preguntó por la forma que cualquier teoría de variables ocultas debía tener. Alcanzó la conclusión de que cualquier teoría de variables ocultas anticiparía unos resultados contradictorios a los que anticipa la teoría cuántica, cuando ambas teorías examinan el mismo tipo de experimentos que familiarmente se denotan cómo experimentos de Alice y Bob. Este resultado significo un duro golpe para los que mantenían la postura de que el universo debía de ser al fin y al cabo determinista.

Pero no se desanimen, en el presente texto vamos a presentar un ejemplo de teoría de variables ocultas, que ofrecen los mismos resultados que la teoría cuántica cuando se evalúan en el experimento de Alice y Bob. Porque al fin y al cabo, Bell no habría tenido en cuenta todas las posibilidades. Comencemos explicando el experimento de Alice y Bob.

3. EL EXPERIMENTO DE ALICE Y BOB

Tenemos en el centro del montaje una fuente de fotones, que lanza dos fotones con la misma polarización plana cada vez, uno hacia el detector de Alice y otro hacia el detector de Bob. Cada detector admite tres posiciones según lo decidan libremente Alice y Bob; pueden colocarlo en posición de detectar si el fotón es capaz de pasar por un filtro horizontal, vertical u oblicuo-derecha. Oblicuo significa a 45 grados

Figura 1: Montaje del experimento Alice y Bob. El emisor central lanza fotones de la misma polarización hacia los experimentadores, que pueden decidir con independencia cuál de los tres filtros pueden utilizar.

Un fotón polarizado plano es como una carta de correos y los filtros de Alice y Bob son como buzones; solo pasarán por la rendija del buzón si entrar correctamente alineados. Pero hay algo más debido a la rareza de la mecánica cuántica, está visto y comprobado que el fotón entra el 50% de las veces por un buzón que está oblicuo. En resumen el comportamiento de los fotones polarizados en una dirección dada es la siguiente:

1. Pasa el 100% de las veces por un filtro paralelo a esa dirección.

2. Pasa el 0% de las veces por un filtro perpendicular a esa dirección.

3. Pasa el 50% de las veces por un filtro oblicuo a esa dirección.

En cada tirada de fotones Alice y Bob elijen cada uno al azar que clase de filtro poner, y comparan entre ellos los resultados que han obtenido. Si en ambos casos el fotón ha pasado o el fotón no ha pasado, dicen que sus resultados coinciden, si en un lado el fotón pasa y en el otro no pasa, sus resultados no coinciden. Si en una tirada sus resultados coinciden apuntan un 100 en el resultado, si no coindicen apuntan 0. Este es el experimento de Alice y Bob tal como lo hemos adaptado.

4. QUE DICE LA TEORIA CUANTICA SOBRE EL EXPERIMENTO ALICE Y BOB

Para solucionar el problema se recurre a una matriz que resume las distintas opciones que tienen Alice y Bob para elegir la orientación de los filtros. Que son tres opciones independientes cada uno, esto hace que en total existan 9 posibilidades.

Tabla I: Matriz para resolver el problema. Para cada tipo de fotón emitido hay una matriz, en su interior se va apuntado la puntuación cuando Alice y Bob eligen entre los distintos filtros.

Por otra parte el fotón puede salir con cualquier polarización plana, esto quiere decir que podría estar girado en cualquier ángulo, pero vamos a simplificar el problema asumiendo que los fotones solo pueden emitirse de una determinada forma:

1. Se emiten polarizados en vertical.

2. Se emiten polarizados en oblicuo-derecha.

3. Se emiten polarizados en horizontal.

4. Se emiten polarizados en oblicuo-izquierda.

Son cuatro formas de emitir fotones, por tanto el experimento tiene 4 matrices, y como son 9 formas de colocar los filtros, tenemos 4 x 9 =36 posibles escenarios que se presentan con idéntica probabilidad. En cada escenario Alice y Bob apuntarán una puntuación, y al final prorratearán la puntuación para los 36 escenarios y obtendrán la puntuación media esperada. Nosotros vamos a anticiparnos resolviéndolo según las pautas de la mecánica cuántica. Para calcular la puntuación para cada escenario hay que tener en cuenta lo que dijimos sobre el comportamiento del fotón cuando se enfrenta a un filtro.

Vamos a ir rellenando la matriz caso a caso. Si los fotones son verticales, y Alice y Bob eligen ambos filtro vertical, el fotón siempre pasa y sus resultados siempre coinciden y ponemos 100 en la casilla. Para el mismo par de fotones, cuando el filtro de Alice es oblicuo-derecha y el de Bob vertical, el fotón siempre pasa por el filtro de Bob pero solo la mitad de las veces por el de Alice. Por ello la mitad de las veces sus resultados coincidirán apuntando 100 y la mitad de las veces no y apuntarán 0. Haciendo que el resultado esperado para esa casilla sea 50.

Si continuamos de este modo por el resto de las 34 posibilidades, habremos rellenado las 4 matrices, y si hacemos la suma de todos los números de la matriz y lo dividimos entre 36 tenemos la puntuación media esperada para el experimento Alice y Bob según la mecánica cuántica. Que es 52,8.

Tabla II: Las matrices con las puntuaciones esperadas por la mecánica cuántica para los 36 escenarios posibles. La media de estas puntuaciones es 52,8.

5. LAS VARIABLES OCULTAS DE JOHN S.BELL

Ahora vamos a pasar a estudiar el experimento desde la perspectiva de John S.Bell de variables ocultas. Desde esta perspectiva clasificar los fotones como de polarización vertical, oblicuo y horizontal es algo obsoleto y superado por unas variables ocultas que determinan exactamente y sin dejar nada al azar cómo se comporta el fotón frente a cada filtro. Sigue habiendo 9 posibilidades totales de cómo pueden estar configurados los detectores en el experimento, lo que cambia es el modo en que se describe un fotón y las diferentes posibilidades que existen de emitirlos.

En total vamos a tener 8 distintos fotones posibles que se presentarán con la misma probabilidad; vamos a tener un fotón que puede pasar por los 3 filtros, un fotón que puede pasar por el vertical y el horizontal pero no por el oblicuo-derecha, otro que no va a pasar por ninguno y así hasta las 8 posibilidades.

Ahora el experimento Alice y Bob pasa a tener 8 matrices y 8 x 9 = 72 escenarios diferentes. Cómo hicimos en el caso anterior pasamos a evaluar la puntuación esperada para cada escenario.

Cuando el fotón es de los que pasan por todos los filtros, y Alice y Bob tienen sus filtros en vertical, los fotones pasa por ambos y sus resultados siempre coinciden. Apuntamos 100 en la casilla. Cuando el Alice tiene el filtro en horizontal y Bob en vertical, el fotón sigue pasando por ambos y vuelven a apuntar 100 en la casilla. Continuamos hasta rellenar los 72 casilleros y prorrateamos para obtener la puntuación media según variables ocultas. ¡Qué sorpresa! es de 66,7.

Tabla III: Las matrices con las puntuaciones esperadas por una teoría de variables ocultas para los 72 escenarios posibles. El texto VXX en la parte superior izquierda significa que se trata de la matriz para el fotón que puede pasar por el filtro vertical y no por el filtro horizontal ni por el oblicuo-derecha. La puntuación promedio es de 66,7 y el promedio de ninguna matriz baja de 55,6.

Está claro que hemos tenido en cuenta fotones que no pasan por ninguno de los filtros y que quizás si los quitáramos el prorrateo podría reducirse hasta 52,8. Pero esto es imposible, puesto que la menor puntuación que puede sacar cualquier tipo de estos fotones deterministas de 55,6. Esta diferencia entre la puntuación mínima que se obtiene entre una teoría de variables ocultas, y la mecánica cuántica, es lo que se mundialmente se conoce como la desigualdad de Bell.

6. UN MODELO DE VARIBLES OCULTAS QUE IGUALA EL RESULTADO DE LA MECANICA CUANTICA

Si el mejor modo de demostrar el movimiento es moviéndose. Vamos a demostrar que existe un modelo de variables ocultas que arroja 52,8 de resultado, creándolo. Para ello vamos a definir nuevamente el comportamiento de los fotones de acuerdo a este nuevo modelo.

1. Los fotones tienen 4 polarizaciones planas posibles; vertical, oblicuo-derecha, horizontal y oblicuo-izquierda. Ya dijimos que en realidad tienen cualquiera, pero sigamos con esta simplificación planteada al principio del texto.

2. Un fotón polarizado en una dirección cualquiera, pasara siempre por el filtro que coincida esa dirección y no pasara nunca por un filtro que este a 90 grados a esa dirección.

3. Existe el Gen Z, que un fotón puede tener o no, y que si lo tiene le permite atravesar un filtro colocado a 45 grados. El Gen Z es una variable oculta y por ello no sabemos ni cuál es el mecanismo ni cómo termina un fotón acarreándolo, pero suponemos que es un proceso determinista. Lo que sí sabemos es que existe una probabilidad del 50% de un fotón lo lleve y que es fácil que lo pierda o gane.

4. Los fotones emitidos por la fuente en una tirada son idénticos en polarización, pero no tienen por qué ser idénticos en cuando a portar o no el Gen Z. Uno de los fotones puede llevar el Gen Z y el otro no, este un aspecto completamente independiente.

Con esto ya estamos preparados para abordad el experimento de Alice y Bob. Cada uno de ellos sigue teniendo tres formas de elegir sus filtros, lo que hacen 9 posibilidades en total.

Sabemos que tenemos fotones con 4 posibles polarizaciones. Preguntémonos ahora de cuantas formas diferentes puede emitir pares de fotones con polarización vertical la fuente. Puede emitir un fotón con Gen Z hacia Alice y otro con Gen Z hacia Bob, un fotón con Gen Z hacia Alice y otro sin Gen Z hacia Bob, etc. Son 4 formas distintas de emitir para la polarización vertical, con lo que en total hay 4 x 4 =16 posibilidades distintas de emisión de fotones y 16 matrices. Haciendo un total de 9 x 16 =144 escenarios para el experimento Alice y Bob, cada uno con su puntuación esperada.

Una vez más calculemos un par de ellas a modo de ejemplo. Supongamos que la fuente ha emitido dos fotones verticales ambas con el Gen Z y que tanto Alice cómo Bob han elegido filtros oblicuo-derecho. Cómo ambos portan el Gen Z, pasara por ambos filtros oblicuos y apuntaran 100 en la casilla. Sin cambiar los filtros, veamos que pasa ahora con la matriz en la que los fotones son ambos verticales pero solo el fotón de Alice tiene Gen Z; el fotón de Alice pasara por el filtro oblicuo, pero nunca lo hará el de Bob y apuntaran 0 en esa casilla. Continuando de esta guisa con los 144 escenarios, y haciendo media de las puntuaciones obtenemos 52,8. Consiguiendo lo que según el planteamiento de Bell, tendría que ser imposible.

Tabla IV: Las matrices con las puntuaciones esperadas el modelo del Gen Z. El texto _XZ en la parte superior izquierda significa que se trata de la matriz para fotones de polarización horizontal, donde solo el de Bob tiene Gen Z. La media de todas las puntuaciones es 52,8 coincidiendo con lo esperado por la mecánica cuántica.

7. CONCLUSIONES

El resultado obtenido, abre de nuevo una puerta que parecía cerrada a la existencia de una realidad oculta aun no anticipada, que potencialmente puede permitir un universo que sea determinista y aunque no lo hemos mencionado en el presente texto, que sea compatible con que la información no viaje más rápido que la velocidad de la luz. ¿A quién no le reconforta esto?

ÉL TIEMPO QUE LE QUEDA A LA ESPECIE

 

Hay un película que se llama <<The Cube>> en donde unas personas están atrapadas en un laberinto, del que no saben cómo han llegado y apenas intuyen cómo funciona. Según van atravesando las salas, encuentran una en donde yace muerto un físico, y en cuya pared hay apuntado un número tras unos cálculos. Al parecer es el tiempo que le queda al laberinto antes de colapsarse. Resulta extraordinario que los datos de un evento tan significativo y al parecer tan desconectado del resto, puede obtenerse a partir de unos datos cotidianamente dispuestos. La presenta exposición recuerda esto mismo.

PLANTEAMIENTO

Supongamos que existe una fabrica que durante su vida útil ha fabricado Terminators. Siendo que cada Terminator fabricado se preguntaba cuando habría de cerrar la fabrica. Suponiendo que en total se fabrican N robots, el Terminator fabricado numero Z, deduciría que existe 1/2 de probabilidad de que haya sido fabricado antes que N/2 y 1/2 de probabilidad que haya sido fabricado después de N/2.

EL JUEGO Y LAS GANANCIAS

Supongamos también que a cada robot acudía un apuntador de apuestas que tras decirles su número de fabricación, les preguntaba por el número total de robots que pensaban que se irian a fabricar en total. Si el robot acierta la penalización es cero, sino acierta la penalización es igual a la diferencia entre N y el numero que diga el robot. ¿Cuál es el número que deberá elegir cada robot para minimizar las penalizaciones?

 

El área en azul es la penalización. Se trata por tanto de calcular la pendiente m que minimiza el área. Una vez que se obtiene la expresión algebraica del área se calcula el punto en el cual su derivada se hace 0:

Pues bien, los robots minimizarán las penalizaciones si hacen N=Z·(2)^(1/2), o si consideran que antes que ellos se han fabricado el 71% de los robots, y solo queda el 29% por fabricar.

CASO HUMANO

Se trata pues de extrapolar el ejemplo del robot y la fabrica, al humano y a la humanidad. Si la extrapolación pudiera hacerse de forma directa y sin mayor detalle, teniendo en cuenta han nacido unos 110.000 millones de homo sapiens hasta ahora, quedarían solo otros 32.000 millones por nacer antes del fin.

FECHA DEL FIN DEL MUNDO

Actualmente el número de nacimientos es X=133 millones por año. Dado que se trata de determinar el tiempo que le queda a la especie, es necesario establecer la forma que adquieren los futuros nacimientos. Para ello consideraremos los siguientes escenarios:

1 La tasa de natalidad se mantiene constante a lo largo de tiempo hasta un cataclismo final

En este caso a la humanidad le quedarían 32.000/133 = 241 años y se acabaría el 2015+241=2256 D.C

2 El numero de nacimientos crece de manera exponencial tal y cómo ha venido sucediendo.

Se supondrá que el aumento en el numero de nacimientos es proporcional al aumento en la población mundial.

Año	Población
a 2014	7181970114
b 2013	7101880810
(a-b)/b	0,0113

Con lo que la expresión del numero de nacimientos a lo largo del tiempo es, en millones:

Lo que marcará el fin de la especie, será cuando el numero de nacimientos llegue a los 32.000 millones. Bastará con integrar la ecuación anterior y encontrar el Y para el cual se igualan.

Por tanto el fin de mundo sería el 2015+117=2132 DC. Y la población mundial final en millones sería de:

 

3 El comportamiento a partir de ahora será la de una reducción paulatina de la población hasta su extinción

En este caso se produciría una disminución gradual de la población. Por tanto debe de producirse una disminución de 7.181 millones mientras nacen 32.000 millones. Esta vez seguiremos la evolución de la población mediante iteraciones en una hoja de cálculo.

Para hacer el calculo supondremos que el numero de nacimientos que quedan es proporcional a la población queda por nacer. El numero de nacimientos de un año será proporcional asimismo a la población de ese año. Con esto en mente puede construirse la siguiente tabla:

 

	A	B	C	D
1	AÑO	POBLACIÓN	NACIMIENTOS	N.RESTANTES
2	2015	7181000000	133000000	=32000000000-C2
3	=A2+1	=B$2*D2/32000000000	=C$2*D2/32000000000	=D2-C3
4	=A3+1	=B$2*D3/32000000000	=C$2*D3/32000000000	=D3-C4
5	…….	…….	…….	…….

Ejecutando las iteraciones obtenemos:

EL CRITERIO DE LOS VOLÚMENES EN EL ESPACIO DE FASES Y SU SUPERIORIDAD AL CRITERIO DE OCKHAM

Introducción
 

Supóngase que se tiene un hecho dado (las manzanas caen) y dos hipótesis pendientes de ser juzgadas que pretenden dar explicación al mismo (la gravedad por un lado o la tendencia natural de las manzanas de cumplir su ciclo vital yendo hacia tierra por otro). Adicionalmente, sucede que es imposible presentar en el juicio experimentos que no se encuentren ya realizados, no existiendo la posibilidad de diseñar un futuro experimento que invalide una de las hipótesis.

Si no existen datos suficientes como para invalidar una de las 2 hipótesis juzgadas, debido a que las dos pueden dar explicación a los fenómenos atendidos, el principio de la Navaja de Ockham establece que es preferible la hipótesis más sencilla sobre la más elaborada a la hora de seleccionar una de las dos hipótesis. Lo cual podría enunciarse como que la hipótesis preferible es la que tiene un menor coste computacional; aquel cuyo algoritmo es más rápido de procesar por una arquitectura computacional dada.

Aunque dos hipotéticas teorías puedan ser equivalentes a la hora de explicar los fenómenos considerados, sino son exactamente equivalentes no ofrecerán las mismas respuestas en toda la gama de cuestiones que se les es posible plantear. Por tanto elegir adecuadamente entre las dos hipótesis aquella que será teoría aceptada, tiene consecuencias en cuanto al conocimiento que se tiene del mundo.

En este texto se planteará un criterio diferente al de la navaja de Ockham para resolver los juicios en los que dos hipótesis de este tipo se pueden ver cautivos. Por otra parte será necesario presentar conceptos como el espacio de fases o la subordinación de teorías para asentar la exposición.

Algo sobre el espacio de fases
 

El espacio de fases es una idea nacida en el desarrollo de la mecánica clásica. Se trata de un volumen  inmerso en un espacio de infinitas dimensiones, en donde uno solo de sus puntos describe completamente el estado físico de todas las partículas del  universo. O dicho de otro modo, en donde cada punto describe un posible fotograma del universo.

Dentro del espacio de fases se pueden formar volúmenes que agrupen puntos que corresponden a fotogramas indistinguibles en cuando dan la misma respuesta a alguna medida realizada por algún aparato o que son equivalentes en cuanto responden de igual modo a una descripción. Estos volúmenes se denominan macroestados, siendo los puntos que contienen los microestados.

El universo evoluciona de un fotograma al siguiente, o de un punto del espacio de fases a otro. Se puede decir que la evolución temporal de un macroestado Z, es una aplicación que transforma el volumen Z en otro volumen Z’. El aumento constante de la entropía impone que ||Z’||>||Z||.
 

La Subordinación de Teorías 

Las teorías sobre el mundo pueden agruparse en escalas, las teorías de más baja escala son aquellas que trabajan a un nivel más fundamental y las que caracterizan un sistema cualquiera con el mayor número de datos. Actualmente en esta escala se encuentra el Modelo Estándar de la física de partículas. En una escala superior a las teorías fundamentales se sitúan las teorías cada vez más generalistas, en donde toman importancia las aproximaciones y cualidades emergentes del comportamiento de la materia a mayor escala. La química y a fisiología animal son respectivamente teorías de mayor escala que la física de partículas

Cualquier nueva hipótesis sobre los sucesos de más alta escala  debe ser congruente con teorías de baja escala que se encuentran aceptadas. Las teorías que están más altas en la escala no pueden modificar las teorías fundamentales, las predicciones de una teoría de alta escala deben de ser consistente con las predichas en baja escala. Ninguna hipótesis de la sociología puede contravenir a las de la biología, ni estas a las de la física.

Criterio de los volúmenes en el espacio de fases (CVEF)
 

Se presentará el criterio que será puesto en comparación con el criterio de Ockham a lo largo del texto. Este criterio debe de aplicarse en la versión maximal o minimal dependiendo de si existe una teoría más fundamental que provee de un espacio de fases de partida o no.

Versión maximal del criterio de volumen en el espacio de fases
 

Siendo el caso más común, se aplica cuando existe una teoría más fundamental aceptada. Puede enunciarse de siguiente modo:

Dadas dos hipótesis será preferible aquella que al aplicarse a la totalidad del espacio de fases del pasado, conduce con mayor probabilidad al hecho presente considerado. 

O equivalentemente:

La hipótesis preferible es la que al aplicarla en retrospectiva sobre el hecho presente, abarca el mayor volumen en el espacio de fases del pasado.
 

Dado que cualquier hipótesis tiene una cualidad reconstructiva de la historia, mediante su uso es posible determinar las condiciones del pasado que han podido originar un hecho en el presente. Desde el macroestado presente que contiene el hecho observado X se aplica la hipótesis para determinar los macroestados pasados que están capacitados para generar dicho hecho X.  El criterio CVEF establece que será preferible la hipótesis que proyecta el hecho presente al mayor volumen pasado.

Según CVEF la hipótesis A es preferible porque conduce a un mayor volumen en el espacio de fases pasado.
 

El criterio de Ockham en términos del espacio de fases
 

Traduciendo el criterio de Ockham a términos del espacio de fases, este vendría a decir que la hipótesis preferible es la que proyecta el hecho presente al pasado a un menor coste computacional. Sin ninguna consideración acerca de los volúmenes atribuidos por cada hipótesis.

Según Ockham la hipótesis B es preferible porque determina las condiciones pasadas que dieron lugar al hecho a un menor coste computacional.
 

Diferencia entre CVEF y Ockham
 

Pese a tener enunciados diferentes, y parecer realmente diferentes, pudiera ser que en realidad los criterios CVEF y Ockham fueran equivalentes, que simplicidad y máximo macroestado pasado (en la versión maximal) se presentaran conjuntamente. Se planteará ahora un ejempló en el que no lo son:

Supóngase un universo alternativo que consiste en una habitación cerrada donde existen piezas de construcción esparcidas en su interior. Estas piezas sufren espontáneamente pequeñas sacudidas que las hacen dar saltos y moverse, golpeándose entre ellas a veces. Adicionalmente hay en la habitación un gran bloque formado por piezas de color azul, siendo que las que hay en el suelo son todas de color rojo. Ahora se tienen dos hipótesis a juicio:

1. Al principio las piezas rojas formaban otro bloque pero su agitación térmica los rompió, mientras que las piezas azules están unidas de forma más estable.
2. Al principio las piezas azules no formaban otro bloque, pero la agitación térmica hizo que se construyera dado que liberan energía al hacerlo.

Es trivial que el volumen del espacio de fases del pasado que corresponde con la hipótesis 1 es muchas ordenes de magnitud menor que el que corresponde a la hipótesis 2, dado que hay más configuraciones con piezas desordenadas que ordenadas. Por tanto mediante el empleo del criterio CVEF, debe de prevalecer la hipótesis 2.

A pesar de que a primera vista parece que el criterio Ockham selecciona la hipótesis 1, es difícil establecerlo sin un modo de cuantificar el peso computacional de las propuestas. Para sortear este obstáculo se utilizará un argumento entrópico. A saber; es más difícil programar la formación de un vaso de cristal cualquiera a partir de los fragmentos dispersos, que programar la destrucción de un vaso de cristal en cualquier montón de fragmentos, debido a que se requieren muchas más cifras significativas para la obra de reconstrucción precisa de un vaso. Por contra cualquier empujón reducirá el vaso a fragmentos. Trasladando el argumento al presente experimento de los bloques,  se concluye que el criterio de Ockham selecciona la hipótesis 1. Por tanto ambos criterios no son siempre equivalentes, dado que deciden hipótesis diferentes.

Demostración de la superioridad del CVEF sobre Ockham en la versión maximal
 

Se puede definir superioridad de criterio del siguiente modo:

Un criterio es superior a otro si su probabilidad de acierto es mayor.
 

Se parte de una teoría fundamental aceptada A y de un hecho presente X. La teoría A proyecta el macroestado que contiene el hecho X al macroestado pasado X’. El volumen del macroestado X’ representa también la totalidad del espacio de probabilidades de posibles precedentes de X, siendo que todos los puntos de X’ son equiprobables. Por tanto la probabilidad de que X provenga de un volumen V delimitado en el interior de X’ es P=||V||/||X’||.
 

Se tiene un conjunto de hipótesis de mayor escala (1,2,3…n) que tratan de derivar X desde el pasado, además al proyectar X al pasado producen volúmenes (1’,2’,3’….n’) con probabilidades (||1’||/||X’||,||2’||/||X’||,||3’||/||X’||……||n’||/||X’||). Es trivial que la hipótesis que abarca mayor probabilidad es la de mayor volumen ||n’||. Por tanto el criterio que selecciona hipótesis que tienen mayor probabilidad de ser ciertas es el criterio que selecciona el máximo volumen en el espacio de fases.

Dado que cualquier punto de X’ es origen equiprobable de X, la hipótesis que más volumen abarque en X’ tendrá más probabilidades de ser cierta.

Versión minimal del criterio de volumen en el espacio de fases
 
Se discute ahora si el criterio sigue siendo superior en cuando la teoría aceptada pertenece a una escala mayor, es decir, cuando las hipótesis versan sobre teorías a un nivel más fundamental del de las teorías que se encuentran aceptadas.

En estos casos, son las teorías aceptadas de un nivel más alto las que establecen un espacio de probabilidades X’ a partir del cual se deriva el hecho presente X.  Las hipótesis (1,2,3…n) presentadas sobre el funcionamiento de la escala fundamental deberán de contener a X’ y aportar una nueva totalidad del espacio de fases (1’,2’,3’….n’), en donde a igualdad de capacidad predictiva deberá prevalecerá la ||n’|| menor.

Por tanto la versión minimal de CVEF debe de enunciarse del siguiente modo:

La hipótesis preferible es la que al aplicarla en retrospectiva sobre el hecho presente, genera un espacio de fases con el mínimo volumen total.
 

Demostración de la superioridad del CVEF sobre Ockham en la versión minimal
 

De partida no existe ninguna preferencia por la cual el universo debiera de regirse por una hipótesis determinada, por tanto de origen se acepta la equiprobabilidad Q=1/n de que existan universos con espacios de fases  (1’,2’,3’….n’). La teoría aceptada impone que X’ debe de estar contenido en los (1’,2’,3’….n’) considerados. La probabilidad de que X’ suceda en n’ es ||X’||/||n’||. La probabilidad de que sucedan X’ y n’ a la vez es P=||X’||/(n·||n’||). Por tanto en cuando unos observadores certifican que existe un pasado X’, mayor será la probabilidad que atribuirán a estar contenidos en un universo n en tanto en cuanto menor sea ||n’||.

Dado que los universos regidos por 1’ y por 2’ son equiprobables, una vez se presenta X’ es más probable que se presente en el universo en donde más volumen ocupa.
 

CVEF o Ockham en la primera teoría
 

En los casos anteriores siempre se ha utilizado como pivote una teoría ya existente, sea esta de alto o de bajo nivel. Pero el pivote no existe en cuando se trata de decidir la utilidad de CVEF en seleccionar la primera hipótesis. Podría decirse que el dilema se presenta en elegir entre una teoría simpe o una teoría estable. Pero es posible solucionarlo.

Para salvar este problema se postulará la construcción de un Metaespacio de fases M, el cual contiene todas las permutaciones de toda posible ordenación de información, que incluye por tanto cualquier universo imaginable a modo de macroestados del mismo, siendo cada uno de sus puntos equiprobables. Dado el hecho presente X y un conjunto de hipótesis igual de efectivas que conducen a pasados de diferente volumen (1’,2’,3’….n’), la probabilidad de que provenga de uno de ellos es mayor cuando mayor es ||n’||. Por tanto aplicar CVEF es también criterio superior a Ockham en primera teoría. La demostración en este caso es semejante a la de la versión maximal.

Otros criterios
 

Aunque en el texto se han confrontado CVEF y Ockham, dado que CVEF es equivalente al criterio que selecciona la hipótesis que tiene más probabilidades de ser cierta, es por tanto superior a cualquier otro criterio, en tanto a superioridad se defina en términos de probabilidades de acierto.

FUGA EN EL MODELO DE RICARDO DEL COMERCIO INTERNACIONAL

 

El modelo de Ricardo que data de un relativamente tempranero 1817 es un constructo racional que permite dilucidar en clave favorable el establecimiento del comercio internacional. Un hecho muy importante que respalda este modelo es que es indiferente que exista un país que sea capaz de fabricar cualquier cosa a un coste mucho menor, que incluso los países menos eficientes salen siempre beneficiados del comercio internacional. Esta conclusión, que es correcta en el modelo, descansa sobre la asunción de que cada país obtiene de forma gratuita unos factores de producción que son intransferibles y que pueden producir sin más vino o pan.

Haciendo un añadido

Ineludiblemente, si los factores de producción se valoran en términos de factores intransferibles, él modelo de Ricardo conduciría  a la aceptación del comercio internacional, ahuyentando cualquier fantasma que pudiera aparecer sobre la verdadera bondad que pudiera tener en los países. No obstante cuando los factores de producción son transferibles, la situación puede cambiar completamente.

Ejemplo didáctico

Se tienen dos países que pueden fabricar mesas o sillas. La mano de obra se considera intransferible, habiendo 100 € de mano obra por país, y la estructura de costes es la siguiente:

coste mano de obra	Sillas	Mesas
Marte	2	2
Júpiter	5	3

Sin tener en cuenta más factores, Marte fabricará sillas y Júpiter Mesas, saliendo ambos ganando del comercio internacional. Pero añadamos un nuevo factor que es transferible; la madera. Siendo que hay 100€ de madera por país, la estructura de costes es la siguiente:

coste en madera	Sillas	Mesas
Marte	4	4
Júpiter	7	5

Dado que ahora la madera es comercializable y Júpiter parece derrocharla demasiado en su proceso de fabricación, la solución que aporta la máxima producción puede pasar por que Marte le compre toda su madera a Júpiter y fabrique todos los muebles. Este es un problema resoluble dentro del método Simplex.

• Cuando la madera no se puede comerciar la solución es que marte fabrica 25 sillas y Júpiter 20 mesas
• Cuando la madera se puede comercializar la solución es que marte fabrica 50 mesas o sillas.

Se ve por tanto que la solución de mayor producción pasa por que Júpiter no fabrique nada en absoluto. Es más, cuando se liberaliza el mercado de madera Marte pasa a fabricar 25 sillas extra, por tanto puede entregar 25 sillas por cada 100 de madera que compra sin entrar en perdidas. Mientras que los productores de Júpiter solo pueden pagar 100/7=14,28 sillas por cada 100 de madera que compran, siendo que los propietarios de la madera venderán a Marte.

En definitiva Júpiter se queda sin dar salida a su mano de obra y vendiendo sus factores de producción comercializables hasta agotarse.

PRINCIPIO DE EXCLUSIÓN, TIPOS DE INTERES, INFLACIÓN Y CARRY TRADE

 

Planteamiento

Es ampliamente aceptado que cuando un banco central incrementa el tipo de interés de la moneda, ello posiciona la economía en un escenario más inflacionista que cuando lo reduce. Esto se justifica argumentando que los bancos comerciales estarán dispuestos a pedir prestado más dinero al banco central dado que serán capaces de hacer rentables una mayor cantidad de inversiones de todas las posibles inversiones imaginables. Dado que las inversiones en vías de realizarse compiten por acaparar los mismos recursos escasos, en un principio cabe esperar un incremento de los precios y por tanto inflación. Sin embargo en el texto se encontrarán argumentos en el sentido contrario.

Sobre el rendimiento positivo esperado de las inversiones

No obstante dado que toda inversión económica rentable genera bienes comerciales por un monto superior al valor de la inversión, se aumenta la oferta del mercado en una cuota superior a la base monetaria insuflada, con lo que en segunda instancia provoca deflación. Es de esperar que en una situación estacionaria en donde conviven inversiones jóvenes y las ya maduras, la tasa de inflación sea menor en cuanto menor sea el tipo de interés. A modo de ejemplo ilustrativo, invertir en una fábrica de alfileres genera deflación en los precios después de la inflación primera en el coste de los ladrillos. Claro está que se ha supuesto que el dinero del crédito es destinado íntegramente a inversión, lo cual no es necesariamente cierto.

 

Anécdota: los tipos de interés y la inflación han tenido una correlación positiva en Japón. Aunque los tipos se fijan en función de la inflación, según lo expuesto esta práctica retroalimenta positivamente la tendencia

 

El agotamiento del tipo del interés y el Quantitative Easing QE

La reducción del tipo de interés de una moneda por parte de la autoridad monetaria conduce a un incremento de las deudas en dicha moneda al hacer viables una mayor cantidad de inversiones. Una vez que la flexibilidad de la política monetaria se considera agotada, aún es posible incrementar el monto de los prestamos mediante las herramientas denominadas Quantitative Easing. Llegados a este punto los bancos centrales compran directamente bonos estatales cuyo resultado es asimismo  la reducción de sus costes de financiación y un incremento de las inversiones realizables por los estados. Ambas políticas incrementan el monto total de las inversiones, incorporando masa monetaria nueva al sistema.

La permeabilidad de la moneda a la demanda agregada

No todo dinero afecta igual en la tasa de inflación ligada a los bienes y servicios, o en su participación en la demanda agregada de bienes y servicios DA. Cada agrupación monetaria M tiene una constante K tal que dDA/dt=M·K. Esto es, el dinero que se guarda en los bolsillos tiene una capacidad de participar en la demanda agregada por unidad de tiempo proporcional a una constante K, que es además bastante superior a la K1 de los dineros perdidos en los entresijos del sofá.

Es necesario distinguir estos dineros en una clasificación según su permeabilidad K a la demanda agregada. Una cantidad de dinero puede encontrarse libre (alto K), cómo en el bolsillo de un ciudadano con ganas de gastar o ligada cómo contraparte (muy bajo K). Mientras que el dinero libre puede utilizarse en contrapartida de un bien cualquiera y participar de forma inmediata en la demanda agregada y en la inflación, el dinero que está ligado no puede ya participar en una nueva transacción. Estas son las denominadas garantías, incluidas las propias de la reserva fraccionaria de los depósitos, las propias de los derivados o del mercado de divisas Forex.

Adicionalmente a esta clasificación del dinero en cuanto a su intercambiabilidad, existe la ordinaria propia de los agregados monetarios (M0,M1-M0,M2-M1-M0,…) los cuales también tienen sus propias constantes K de permeabilidad a la demanda agregada DA. En general cuando más bajo M más cerca está del consumo y por tanto participa en mayor medida a la demanda agregada.

Las inversiones en diferentes superficies de permeabilidad a la DA

Los mercados de productos financieros de todo tipo son tan susceptibles a la inversión cómo una fábrica y unas máquinas lo son. No obstante mientras que el gasto de las inversiones fabriles suponen un aumento de la demanda agregada, el gasto en las inversiones financieras parecen tener la cualidad de permanecer cautivas en la topología de la economía financiera, siendo que sus efectos inflacionarios en la economía productiva son menores.

De hecho se utilizará el valor de K de los dineros que participan en una inversión para clasificar estas inversiones en:

• Inversiones en la superficie permeable a la DA, (SP)
• Inversiones en la superficie poco permeable a la DA, (SPP)

La divisa de la nación

La divisa nacional suele estar presente en mayor medida que cualquier otra en la demanda agregada de una nación, así en Europa la demanda agregada está construida mayormente en Euros, aunque también pueda comprarse con otras fórmulas dado el caso. Por tanto la divisa nacional es mayoritaria en la SP. Pero no sucede lo mismo con la SPP de la nación, en donde por ejemplo la divisa Euro puede tener y tiene menor hegemonía, compartiendo su espacio con una cesta de divisas que incluye Dólar, Libra, Yen, etc.

La divisa preferida para la inversión

Existen preferencias en cuando a endeudarse en una moneda con bajos tipos de interés a la hora de realizar una inversión. Se llama carry trade cuando una divisa se sustrae de su ámbito nacional para financiar inversiones en otro lugar, para ello se cambia la moneda en el que se tiene el préstamo por moneda local que tendrá un mayor tipo de interés y se vuelve a comprar la moneda de bajos tipos para terminar de pagar el préstamo . Estos movimientos se realizan entre divisas de diferentes continentes en microsegundos.

El efecto desplazamiento de las divisas por cambio en tipos, principio de exclusión

Cuando una moneda reduce sus tipos de interés, pasa a ocupar las superficies poco permeables de las inversiones de todo el mundo, desplazando a la divisa con mayor tipo que se encontraba en ese lugar y empujándola a la superficie permeable de su nación. Esto sucede porque la superficie impermeable a la DA es por contra la más permeable al tráfico internacional de divisas.

 

Efecto desplazamiento; una bajada de tipos en A conduce a la sustitución de otra moneda B en la superficie de las inversiones impermeable a la DA.

Por tanto una bajada en los tipos de interés provoca un aumento de la masa monetaria permeable fuera de la nación del banco central (BC). El consiguiente incremento en la DA genera inflación al aumentar el consumo y no produce mayor tasa de inversión hasta que no logre revisar los tipos a la baja.

Por contra, cuando un banco central aumenta el tipo del dinero, ello hace que su divisa sea desplazada por otra en la superficie impermeable, conduciéndola hacia la permeable, aumenta la masa permeable, la DA y provocando inflación. Esta es la segunda objeción importante que se presenta al hecho aceptado de que una subida de tipos es contraria a la inflación. Siguiendo el mismo esquema, al bajar los tipos de interés la divisa invade espacios impermeables internacionales, en donde se convierte en demandada, provocando deflación en la nación.

En resumen;  se deben apreciar los efectos comunicantes entre divisas que realiza la superficie impermeable, que junto con la existencia de un principio de exclusión similar al de Pauli configura una mecánica propia del estudio de los acontecimientos.

LA PARADOJA EN LA PREDOMINANCIA DEL 1 EN LA PRIMERA CIFRA DE LAS MAGNITUDES

 

Planteamiento del problema

Supóngase que cuando se hace una medida se obtiene un resultado en números decimales. Se da un hecho muy curioso que puede enunciarse del siguiente modo, en el conjunto de todas las mediciones realizadas hay muchas más mediciones cuya primera cifra es 1 que mediciones cuya primera cifra es 9.

A priori tanto el 9 cómo el 1 tienen la misma probabilidad de ser el primer número de una medida determinada, por tanto debería de haber tantos 1’s cómo 9´s.

Solución

Si tenemos una unidad de medida básica (el metro), y una familia de entidades que podemos medir (montañas),  siempre va ha existir un elemento en esa familia que dé la máxima medida (el Everest). La probabilidad de que aparezca un digito determinado en la primera cifra de la máxima medida es igual para cada uno de los dígitos; 1/9 para cada posibilidad. Cuando la 1º cifra de la medida máxima de una familia es N, se dirá que la familia es de tipo N. Si consideramos varias familias del mismo tipo, la media de las 2 primeras cifras para el máximo de una familia de tipo N es de N5.

Una vez se tiene el máximo de la familia, las mediciones se repartirán con la misma probabilidad entre dicho máximo y el 0. De esta forma se puede saber la probabilidad de que una medida en una de las familias comience con una cifra determinada. Se puede hacer una tabla combinando las diferentes familias para cuando la mantisa es 2 (dos cifras significativas), para conocer la probabilidad de aparición de cada símbolo como primera cifra:

		FAMILIA TIPO
COMIENZA POR		1	2	3	4	5	6	7	8	9	SUMA	%
	1	7	11	11	11	11	11	11	11	11	95	19,67%
	2	1	7	11	11	11	11	11	11	11	85	17,60%
	3	1	1	1	11	11	11	11	11	11	69	14,29%
	4	1	1	1	1	11	11	11	11	11	59	12,22%
	5	1	1	1	1	7	11	11	11	11	55	11,39%
	6	1	1	1	1	1	7	11	11	11	45	9,32%
	7	1	1	1	1	1	1	7	11	11	35	7,25%
	8	1	1	1	1	1	1	1	7	11	25	5,18%
	9	1	1	1	1	1	1	1	1	7	15	3,11%

De este modo se explica la abundancia del 1 como primera cifra.