El problema surge de plantearme como seria digamos un sistema solar si estuviera contenido en la superficie de una esfera, realizare un análisis tomándome la libertad de realizar algunas aproximaciones que simplifiquen el trabajo. Las condiciones de estabilidad para otro tipo de orbitas, no son objeto de este articulo, pese ello el resultado es tan extenso como tedioso, de difícil seguimiento pese a las numerosas figuras e interludios (nunca suficientes) para aquellos que no estén entrenados, por ello les recomiendo que no lo lean y si eso contemplen esas entretenidas graficas que eran el medio para la comprensión que pretendía.
SE SUPONE
- Se supone una masa inscrita m sobre la superficie de una esfera de perímetro D.
- Se supondrá que la influencia gravitatoria esta contenida sobre la superficie de la esfera.
- Se supondrá que la influencia gravitatoria recorre indefinidamente toda la esfera.
EL CAMPO GRAVITATORIO EN LA SUPERFICIE
Para cualquier punto de la esfera es posible trazar un circulo máximo C que pase por la masa. Si situáramos una masa hipotética en cualquier punto de la superficie la fuerza resultante se obtiene de restar las dos fuerzas de sentido contrario que aparecen par cada una de las 2 geodesias del círculo máximo. D2 es la geodesia mayor y D1 la menor. En vez de situar una masa hipotética calculare la expresión del campo gravitatorio para cualquier punto, para ello será necesario sumar las sucesivas "pasadas" del campo.
Tomando:
Planteamos el sumatorio:
Sumatorio convergente. Desconozco como obtener el valor exacto del sumatorio, por inspección los términos decrecen rápidamente para n>0, definiendo Z:
De forma que sumando únicamente el 1º término del sumatorio el error es menor al 6%, por lo tanto trabajaremos con esta función por espíritu mediterráneo.
Se define:
y da una idea de la intensidad del campo gravitatorio si se considerara que la masa actúa sobre un plano y no sobre una esfera.
Representando y´/y:
Se observa naturalmente que según aumenta la distancia el campo se hace más débil con respecto a un plano. En verde el perfil de la esfera como referencia. El campo se anula como es natural en la antípoda.
EQUILIBRIO DE FUERZAS
Supongamos ahora que una pequeña masa hipotética es colocada en la superficie de la esfera y empieza a orbitar describiendo un círculo sobre la masa primera. Sobre esta masa hay que considerar 3 fuerzas:
1º Fuerza gravitatoria debida a la masa grande
2º Fuerza centrifuga con respecto al giro sobre la masa
FUERZA GRAVITATORIA
La fuerza gravitatoria se obtiene mediante la aproximación del campo gravitatorio del apartado anterior:
FUERZA CENTRIFUGA
Esta es la parte mas complicada, un masa cualquiera que se desplaza por la superficie de una esfera sin que se le aplique fuerza tiende a describir un circulo máximo (geodesia).
Fíjense en el ángulo a que utilizare más tarde. Al verse influenciado por la presencia de la otra masa el móvil se desplaza de la geodesia una distancia r en un tramo vt
Este desplazamiento r por cada vt depende de la altura a la que se encuentra la orbita como puede observase en las siguientes vistas
El radio R dado que se trabaja con una esfera unidad y con radianes:
La desviación r es máxima cuando la geodésica en azul esta perpendicular, se denomina r max en tal caso. Cuando t es suficientemente pequeño se cumple que:
Se aprecia que vt,R, y rmax forman un triangulo rectángulo, se puede plantear la siguiente ecuación.
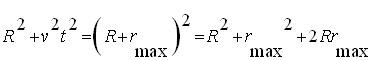
Donde
puede despreciarse para t cortos frente al resto de sumandos por tanto:
Por otra parte de los movimientos uniformemente acelerados:
Donde A es la aceleración centrípeta.
VELOCIDAD ORBITAL
Una masa en orbita resulta del equilibrio entre dos fuerzas
Donde R y D1 son equilicua:
Donde:
Por tanto:
Que representado gráficamente con Gm=1:
En verde la silueta de la esfera y en negro las velocidades orbitales para cada posición sobre la esfera. Se debe de notar que no existen orbitas circulares estables a partir de la mitad de la esfera.
El periodo será:
Que representandolo:
En verde claro el tiempo que tarda en orbitar un móvil según la distancia y en rojo el periodo de un hipotético móvil que se desplaza sobre una superficie plana a modo de comparación.
No hay comentarios:
Publicar un comentario